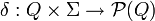Un autómata finito determinista (AFD)
Es un autómata finito que además es un sistema determinista; es decir, para cada estado q ∈ Q en que se encuentre el autómata, y con cualquier símbolo a ∈ Σ del alfabeto leído, existe siempre a lo más una transición posible δ(q,a).
En un AFD no pueden darse ninguno de estos dos casos:
- Que existan dos transiciones del tipo δ(q,a)=q1 y δ(q,a)=q2, siendo q1 ≠ q2;
- Que existan transiciones del tipo δ(q,ε), salvo que q sea un estado final, sin transiciones hacia otros estados.
Un autómata finito no determinista (AFND)
Es aquel que, a diferencia de los autómatas finitos deterministas, posee al menos un estado q ∈ Q, tal que para un símbolo a ∈ Σ del alfabeto, existe más de una transición δ(q,a) posible.
Haciendo la analogía con los AFDs, en un AFND puede darse cualquiera de estos dos casos:
- Que existan transiciones del tipo δ(q,a)=q1 y δ(q,a)=q2, siendo q1 ≠ q2;
- Que existan transiciones del tipo δ(q,ε), siendo q un estado no-final, o bien un estado final pero con transiciones hacia otros estados.
Cuando se cumple el segundo caso, se dice que el autómata es un autómata finito no determinista con transiciones vacías o transiciones ε (abreviado AFND-ε). Estas transiciones permiten al autómata cambiar de estado sin procesar ningún símbolo de entrada.
Formalmente, se distingue de la 5-tupla que define a un autómata finito determinista en su función de transición. Mientras en un AFD esta función se define de la siguiente manera:
en un AFND se define como:
Para el caso de los AFND-ε, se suele expresar la función de transición de la forma:
donde P(Q) es el conjunto potencia de Q.
Esto significa que los autómatas finitos deterministas son un caso particular de los no deterministas, puesto que Q pertenece al conjunto P(Q).
La interpretación que se suele hacer en el cómputo de un AFND es que el automáta puede estar en varios estados a la vez, generándose una ramificación de las configuraciones existentes en un momento dado. Otra interpretación puede ser imaginar que la máquina "adivina" a qué estado debe ir, eligiendo una transición entre varias posibles.
Note finalmente que en un autómata finito no determinista podemos aceptar la existencia de más de un nodo inicial, relajando aún más la definición original.